Mike Pozulp's Blog

Mike Pozulp

February 26, 2020

Using a Neural Network to Solve a Polynomial

Design and execution of an unconventional polynomial solver.

In the fall of 2018 I met a very talented machine learning practitioner who showed me how to solve an integro-differential equation using a neural network. He had considerable experience designing and implementing neural networks as well as knowledge of the theory. This post is a baby step in my pursuit of his knowledge.

Before jumping in to more complicated equations he started with a simple polynomial.

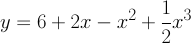
polynomial equation — Equation 1: A polynomial function.

According to the universal approximation theorem, all we need to do to find y is to pass x through a feed-forward network with a single hidden layer. Here is one such network.

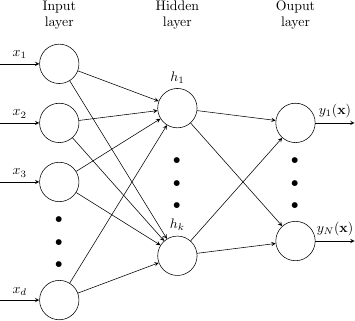
network architecture figure — Figure 1: A fully-connected feed-forward network with a single hidden layer.

Because polynomials are functions there is one y value that corresponds to each x value, so we will use the same number of nodes in the input layer and output layer, meaning d and N will be equal.

Learning with data versus learning an equation

In traditional learning applications like image classification we would partition our image set into training images and test images, select a loss function, and then pass the training images through the network. Learning an equation, by contrast, does not employ a data set. To solve our polynomial we create a single vector of one hundred coordinates on the x-axis uniformly spaced between -3 and 3 which we pass through the network over and over again until we achieve the convergence criterion.

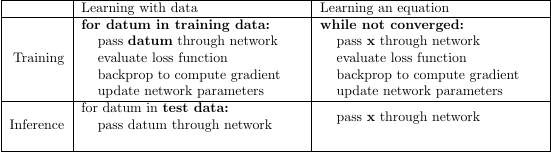
learning algorithm comparison table — Table 1: Pseudocode comparison of learning with data versus learning an equation with differences highlighted in bold.

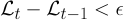
convergence criterion equation — Equation 2: The convergence criterion. t is the epoch index and epsilon is a small, user-defined quantity. When the loss stops changing by more than epsilon we stop training.

Our loss function contains the polynomial that we are approximating. In traditional learning applications a single loss function may be applied to multiple problem domains. Here, because the loss function contains the equation, a different loss function would be necessary for learning a different equation.

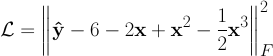
loss function equation — Equation 3: The loss function. Both x and y-hat are bolded to indicate they are vectors. y has a hat to indicate that it is an approximation of the actual polynomial function y. We convert the loss from a vector quantity to a scalar quantity by application of the Frobenius norm.

The optimizer is responsible for updating the network parameters such that the next pass results in a smaller loss. We employ the Adam optimizer, which is a popular variation on stochastic gradient descent.

Learning the polynomial

We use PyTorch to implement our model.

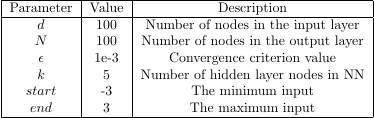
model inputs table — Table 2: Model dependencies.

We provide the extent of the domain when we run the model: "poly.py -3 3". On my Ryzen 5 2400g it takes just 3.5 seconds to converge.

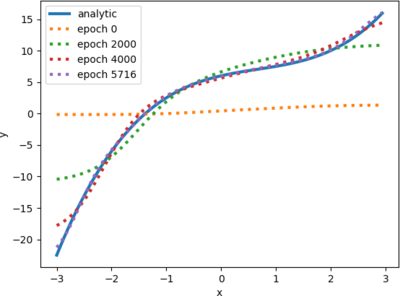
Figure 2: The solution plotted at different epochs. The approximation converges to the analytic solution (Equation 1). The convergence criterion was achieved after 5716 epochs.

loss plot — Figure 3: The loss as a function of epoch. The rate of convergence is highest at the beginning of training and lowest at the end, which means the marginal value of an epoch decreases with epoch, but the decrease is not exactly monotonic. It lurches.

Where to go from here

We could solve more interesting equations, like differential equations, integro-differential equations, and multivariate equations. We could also try to understand our network better with a parameter study where we try changing network qualities. Examples include

learning rate
optimizer
number of hidden layers
number of nodes in the hidden layer(s)
number of nodes in the input/output layers
network connectivity

We could try interpolating and extrapolating. We could also look at the performance profile of the network. We could try using a GPU.

Send me your suggestions. My email is in my resume.

Back